

It’s used to figure out how far two points are apart. That is a sufficient condition for this object to be a parallelogram. A few examples of coordinate geometry applications are shown below. So, we have proven that opposite sides of quadrilateral #PQRS# are parallel to each other. Use your drawing to prove that ABC is an isosceles triangle.

#Coordinate geometry and proof software#
Use dynamic geometry software to draw AB with endpoints A(0, 0) and B(6, 0). #(y_S-y_R)/(x_S-x_R)=(y_C+y_D-y_C-y_B)/(x_C+x_D-x_C-x_B)=#Īs we see, the slopes of #PQ# and #RS# are the same.Īnalogously, slopes of #PR# and #QS# are the same as well. How can you use a coordinate plane to write a proof Writing a Coordinate Proof Work with a partner. For this, let's calculate the slope of both and compare them.
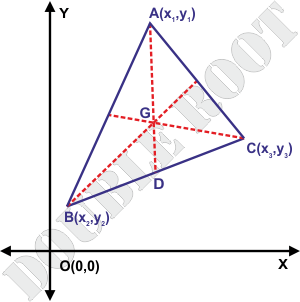
Let's prove that #PQ# is parallel to #RS#. Let four points #A(x_A,y_A)#, #B(x_B,y_B)#, #C(x_C,y_C)# and #D(x_D,y_D)# are vertices of any quadrilateral with coordinates given in parenthesis. The Mid- Point Theorem is also useful in the fields of calculus and algebra. The ‘x’ and the ‘y’ coordinates must be known for solving an equation using this theorem. Midpoints of sides of any quadrilateral form a parallelogram. The theory of midpoint theorem is used in coordinate geometry, stating that the midpoint of the line segment is an average of the endpoints. In some cases to prove a theorem algebraically, using coordinates, is easier than to come up with logical proof using theorems of geometry.įor example, let's prove using the coordinate method the Midline Theorem that states: In other words, we use numbers (coordinates) instead of points and lines. Coordinate proof is an algebraic proof of a geometric theorem.


 0 kommentar(er)
0 kommentar(er)
